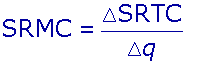3.6 Costs
[3.2 Demand]
[3.3
Price Elasticity]
[3.4 Supply]
[3.5 Production]
In the discussion of production
functions, you saw that firms are able to adjust their inputs in the long run
more easily than they are able to adjust them in the short run. Remember,
quantities of some inputs are fixed in the short run. This lack of flexibility
in the short run has implications for the cost structure of the firm. Your
analysis of a firm's particular cost structure depends on whether you are
considering the firm's short-run decisions or its long-run decisions.

Do you remember the discussion about Groveji? Groveji will provide a
good example for the discussions of short-run costs.
Recall that Groveji
managers were thinking about the costs associated with producing bags of
organic fertiliser. At this point, the managers are considering the total cost
of the inputs they will need to produce the fertiliser. If you assume that Groveji uses only capital (K) and labour (L) in
production, its total cost of inputs will be given by

In this equation, r represents the constant rental
cost of a unit of capital and w
represents the constant wage cost of
a unit of labour.
In the future, Groveji
may build another manufacturing facility, but for now, it has only one facility
to work with. You can assume, then, that Groveji's
capital is fixed at K units in the
short run. If Groveji decides to produce more output,
it must increase its variable input, labour. The costs associated with units of
capital, rK,
are fixed costs. The costs associated
with labour, wL, are variable costs.
The
expression above shows total cost as a function of the quantities of each input
that Groveji uses. This is essentially an accounting
definition—firms incur costs by spending money on inputs. In contrast, much of
the economic analysis of costs concerns the relation between costs and quantities
of output. For instance, if Groveji knows it can sell
100 bags of fertiliser—beyond what it currently sells—for $20 each, will the
sale of these additional bags prove profitable? To answer this question, Groveji must know the cost of producing those additional
bags.
Short-run
total costs
Now,
suppose Groveji managers want to track how the
company's costs change as it produces more fertiliser. To do so, they need to
consider the company's short-run total costs (SRTC). SRTC is the total cost of
producing various levels of output in the short run, when output can change
only when variable inputs change.
The short-run total cost function is
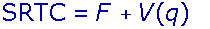
In this equation, F indicates fixed costs, which do not change with output. Rent on a
fixed facility that cannot be subleased is an example of a fixed cost. If Groveji produces 100 bags or 1,000 bags in a day, it must
still pay rent, and the amount of rent it pays won't change just because output
changes. Remember that a firm can incur fixed costs every period; be careful
not to confuse fixed costs with sunk costs.
V(q) indicates variable costs, which change as output
changes because Groveji must use varying amounts of
labour to produce varying numbers of bags of fertiliser.
Click on the following link to find out
how to derive cost functions from production functions.
The
short-run total cost function is useful for calculating the short-run profits
of the firm, which are the revenues of the firm minus the firm's short-run
total costs. Sometimes, however, firm managers want to know costs on a per-unit
basis. You can derive two common types of per-unit costs from the SRTC
function: short-run average cost (SRAC)
and short-run marginal cost (SRMC).
Short-run average cost
Short-run
average cost is the per-unit cost of output at different levels of production.
To find SRAC, divide short-run total cost by output. SRAC interests the firm
because the firm will be profitable if it can sell each unit it produces at a
price higher than the average cost of those units.

Short-run marginal cost
Short-run
marginal cost is the change in short-run total cost generated by a change in
output. Graphically, short-run marginal cost is the slope of the short-run
total cost function and indicates the rate of change in total costs as output
increases. A manager might look at short-run marginal cost to determine whether
or not the firm should expand production. If a firm can sell an additional unit
of output for more than it costs to produce that additional unit (marginal
cost), then the firm should produce that additional unit.
One way to calculate marginal cost is over a range of
output. In this, case short-run marginal cost is defined as
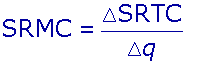
The link here contains advanced
material, which shows how calculus can be used to calculate the SRMC from the
cost function.
The following table illustrates
short-run total, average and marginal costs for a particular total cost
function. Here, the short-run marginal cost is calculated over ranges of
output.
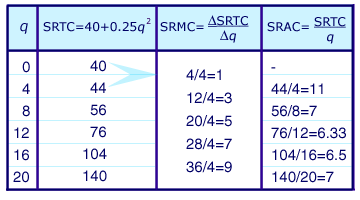
Notice in the table above that SRAC is
11 when q = 1, falls to as low as
6.33 when q = 12, then increases for
higher levels of output. The shape is common for short-run average costs curves
and is often referred to as a U-shaped average cost curve. (You can see an
example of a U-shaped average cost curve below, under Graphical representations
of short-run costs.) It is important to understand the economic reasons for the
shape of the curve.
In the short run, a firm has already
chosen the level of its fixed input and will not change this level, even if
managers want to increase or decrease output. If the firm produces a small
quantity of output, the cost of the fixed input (capital) is spread over a
small number of units, so SRAC is high. If the firm increases its output, the
cost of the fixed input is spread over a greater number of units, so the
average cost per unit decreases. This tendency for SRAC to decrease because
fixed costs are spread over greater output levels will continue as output is
increased but becomes less and less important.
For many production processes, you
expect SRAC to increase eventually due to the law of diminishing marginal
returns. Diminishing marginal returns means that output increases by smaller
and smaller amounts as additional units of a variable input (labour) are used
with a fixed level of another input (capital). Diminishing marginal returns
causes the marginal cost of the additional units of output to increase.
Eventually, the higher marginal cost of additional units offsets the
cost-saving effects described above, leading to the common U-shape for
short-run average costs.
Graphical
representations of short-run costs
You
can also show short-run total, average and marginal costs on a graph.

Notice on the graphs that additional
units of output become increasingly more expensive to produce for this example;
that is, total cost increases at an increasing rate, which means marginal cost
must be increasing. Short-run marginal costs typically increase when output is
high because of the diminishing returns on the variable inputs.

The particular production and cost
functions developed in this section provide a relatively simple example of how a
firm's costs might change depending on the level of its output. Other cost
functions with shapes that differ from those above are possible and, indeed, may
more accurately reflect the costs certain firms face in the real world.
Long Run Costs of Production
In the long run, a firm uses the
combinations of inputs that produce each level of output at the lowest total
cost. Because no inputs are fixed in the long run, the long-run total cost
function (LRTC) will not have a fixed cost component. That is, all costs will
be variable costs. (Remember, in the short run at least one input is fixed so
the short-run total cost function has a fixed component, F.)
The link here contains advanced
material that explains mathematical representations of long-run cost functions.
You can derive a firm's LRAC curve from its individual short-run
average total cost (SRATC) curves. Each SRATC curve depicts a firm's short-run
cost of production when different amounts of capital are used.
The LRAC curve is obtained by taking the lowest SRATC for each
possible level of output—it is the lower envelope of SRATC curves. Thus, the
LRAC depicts the minimum cost of producing any output.
The following animation shows how to arrive at the LRAC curve for ComputerCo.
Economies and
diseconomies of scale
If a firm's long-run average cost is constant, or the same for all
levels of output, then the firm's production efficiency doesn't improve or
worsen as the firm produces more of the good. The firm experiences no economies
of scale.
If a firm's long-run average costs increase at higher levels of
output, then the firm becomes less efficient at producing the good as it
produces more of it. The firm experiences diseconomies of scale.
If a firm experiences lower long-run average costs as it increases
output, then the firm exhibits economies of scale.
It is also possible for a firm to exhibit diseconomies of scale at
high levels of output, but economies of scale at lower levels of output.
For advanced information on how economies and diseconomies of
scale can also be represented mathematically, click the link here.
To
summarise:
·
If LRAC is
constant as output changes, the firm recognises no scale effects.
·
If LRAC
increases as output increases, the firm has diseconomies of scale.
·
If LRAC
decreases as output increases, the firm realises economies of scale.
Economies
of scale often arise in information industries. The link here shows how they
appear in a computer software firm.

![]()
![]()